Author:
(1) Lothar Moeller, SubCom, Eatontown, NJ 07724, USA, [email protected].
Table of Links
GPS Long-Term Stabilized RF Phase Meter
Simple and Accurate models for tides
Latency Variations on Transpacific Cable
Poisson effect on pressurized cables
Conclusions, Acknowledgments, and References
3. SIMPLE AND ACCURATE MODELS FOR TIDES
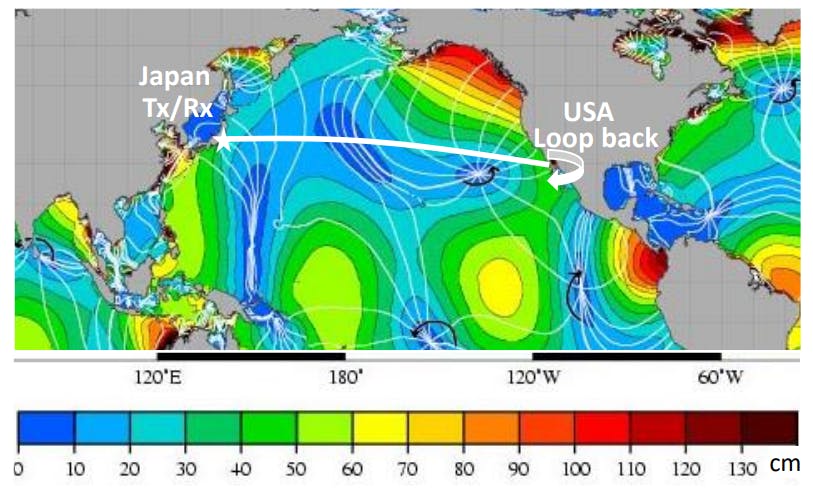
For a qualitative understanding of tidal signatures in our data we introduce a simple earth-lunar system followed by a quantitative analysis based on a tide simulator. The moon orbits the earth, envisioned as a sphere covered with a thin water layer (Fig. 3d). Both precess around their common barycentre. Gravitational, centrifugal, and centripetal forces stand in equilibrium and deform the water surface depending on the lunar position. When they both align with the sun, it maximizes the deformation resulting in two larger water bubbles (known as spring tides). A hypothetical cable connecting the earth’s North and South Pole would then experience higher than average static water pressures when passing underneath these bubbles (semidiurnal, 2x a day). At neap tide
![Fig.2: Dominant amplitudes (M2 constituents) for tides across the Pacific[6],[7] and approximate position of the subsea cable.](https://cdn.hackernoon.com/images/fWZa4tUiBGemnqQfBGgCPf9594N2-29830gn.png)
the proportions differ leading to weaker water elevations. While this simple model provides fundamental insights into the temporary evolution of the static water pressure, multiple factors, including continental boundaries, the ellipticity of the moon and sun’s orbits, and the obliquity of the earth axis, all significantly impact the actual tide dynamics. NASA’s GOT4.7 simulator takes the variables into account when globally computing tide levels with ~1 cm accuracy[6,7] .
This paper is available on arxiv under CC BY 4.0 DEED license.